集成学习总结：GBDT, xgboost方法

OK, 我们在前文中已经讨论过了Boosting的一个算法：AdaBoost，在本文中，我们来看看Boosting族中其他两个重要算法：GBDT和xgboost。

GBDT

GBDT (Gradiennt Boosting Decision Tree) 梯度提升树（以决策树为基函数的提升方法称为提升树）采用的是和AdaBoost一样的线性模型，并通过迭代不断更新权值分布。然而其限定只能使用CART回归树模型，而且迭代思路和AdaBoost也不同。接下来，我们从损失函数选取的角度来讨论下，GBDT和AdaBoost的不同。

在Boosting的迭代中，我们在第$m-1$轮后得到了学习器$[f_1 \cdots f_{m-1}]$，我们希望下一轮的学习器$f_m$能够纠正存在的错误，即

$$f_m(x)=\mathop{\arg\min}_{f}L(f_{m-1}+f|D)$$

其中$L$是损失函数，$D$是训练集。AdaBoost选择了指数损失函数，然后用泰勒公式展开后发现：让$D_m$服从某一分布，即可使得损失函数达到最小 （具体证明可参照西瓜书），这也是为啥AdaBoost要去改变权值分布。而GBDT则不一样，其希望$f_m$能够使损失函数在第$m$轮，走向$m-1$轮中损失函数下降最快的方向。

具体看下GBDT的流程。假设有个回归问题，我们使用决策树作为基学习器。决策树的预测为

$$T(x;\theta)=\sum^J_{j=1}\gamma_jI(x\in R_j)$$

其中$R_j$是区域，$\gamma$是返回值，$I$条件成立情况下为1，否则为0，其中的参数$J$可以大概看做树的深度的一个表示，这是一个待调的参数。那么GBDT解决这个问题的具体流程如下图:

这里等待复习完决策树再进行总结。

Boosting算法也可以用使用的损失函数来归类，如下图：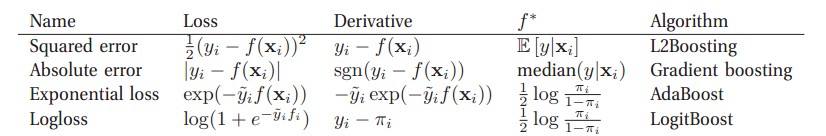
可以看到AdaBoost选取的是指数损失函数，而GBDT选取的是绝对值损失函数。

xgboost

xgboost 的全称是eXtreme Gradient Boosting，由华盛顿大学的陈天奇博士提出，在Kaggle的希格斯子信号识别竞赛中使用，因其出众的效率与较高的预测准确度而引起了广泛的关注。

与Adboost的区别：GBDT算法只利用了一阶的导数信息，xgboost对损失函数做了二阶的泰勒展开，并在目标函数之外加入了正则项对整体求最优解，用以权衡目标函数的下降和模型的复杂程度，避免过拟合。所以不考虑细节方面，两者最大的不同就是目标函数的定义。