今天来总结下硬间隔支持向量机 (Support Vector Machine),由于支持向量机中的对偶问题包含大量的推导,完全用公式码出来太浪费时间,所以我就以总结写提纲的方式来写本文。
现在有一些训练样本,我们想通过在样本空间寻找一些超平面来把他们划分开来。此外,我们还要求该超平面对样本局部扰动的容忍性较好,也就说我们不仅要考虑已有样本,对那些可预见的样本分布,我们也要尽量把他们分离开。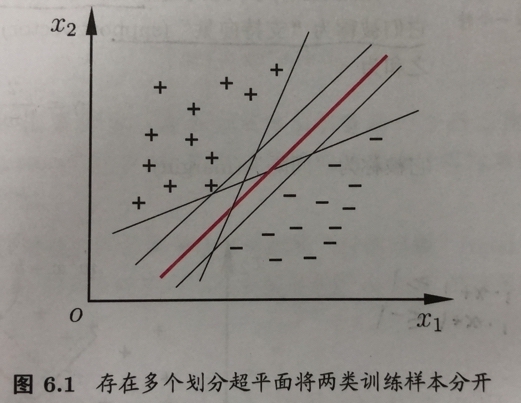
也就是说,我们要尽量选取像图中红色那样的划分区间。
我们一般用$\omega^Tx+b$来描述这一超平面,空间中任意点到超平面$(\omega,b)$的距离可以写成
并可以用向量知识证明。对于一组超平面,如果其能使对于任意$(\textbf{x}_i,y_i)\in D$,有
我们就称它就能够将训练样本正确分类。实际上,{+1,-1}这个取值并不重要,因为一旦能满足上式,其他的值也都能满足。能使上式等号成立的点被我们成为支持向量。然后,我们把优化问题归纳成:
其中$\frac{2}{||\omega||}$指的是两个异类支持向量到划分平面的距离之和。为了简化计算,我们又可以把上式重写成:
经过拉格朗日的对偶问题转换,上述问题可转化为:
省略一堆证明,原理是通过拉格朗日极大极小规约,来推导出上述问题的解相当于其对偶问题的解。但在这里要补充:在对偶问题的转化中,需要满足KKT条件。这种限定,使得模型训练仅受那些最大分割边界上的那些样本的影响,这也就是为什么称他们为支持向量。
假如我们能求出$\mathbf{\alpha}$,我们就可以得到划分超平面的公式:
为啥嘞?因为在省去的对偶问题推导中,有式$\omega=\sum^m_{i=1}\alpha_iy_i\textbf{x}_i$。OK,那咋求$\alpha$呢?周老师云,二次规划算法易解之,(好吧,不懂)。但他又说用SMO求更高效。SMO算法指的是固定一对$\alpha_i,\alpha_j$然后求极值,然后一直迭代到底。具体实现中,SMO先选取一个违背KKT条件最大的值,再选取一个下一个变量,它的样本与上值对应的样本间隔最大。
实际上,划分远远没有这么简单,因为有时候在样本维度,根本不存在这样一个划分空间。很直观的一个想法就是把数据升维。假设,我们找到了合适的维度,这个维度存在对样本$\textbf{x}\Rightarrow\phi(\textbf{x})$的划分空间,可惜的是,高维向量$\phi(x)$的转置和乘积一般都是很很困难的。为了解决这个问题,引入了核函数。我们令核函数为$\kappa(\textbf{x}_i,\textbf{x}_j)={\phi(\textbf{x}_i)}^T\phi(\textbf{x}_j)$。只要一个对称函数所对应的核矩阵半正定,它就能作为核函数使用。我们一般常使用的核函数如下图:
当我们选择一个核函数来作为两样本的高纬度内积后,就有式: